반응형
파이는 단순한 수학 기호가 아닙니다. 끝없는 소수, 반복 없는 수열, 완전하지만 계산 불가능한 파이의 본질을 통해 인간 인식과 철학을 돌아봅니다.
🔍 시작은 이 질문으로:
"끝이 없는 수를 우리는 이해할 수 있을까?"
π는 무한히 이어지는 소수다.
하지만 인간의 뇌는 유한한 구조를 가지고 있다.
그렇다면 우리는 π를 정말 ‘이해’한다고 할 수 있을까?
아니면 단지 외우고, 흉내 내고, 근사치로 다루는 것일까?
∞ 1. 파이는 인간이 감당할 수 없는 무한
π는 소수점 아래 끝도 없고, 규칙도 없다.
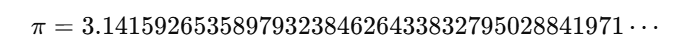
- 무한히 이어진다는 것 = 완전히 이해하는 건 불가능하다는 뜻
- 반복도 없으니 예측하거나 구조화하기 어렵다
- 수학자조차 π를 절대 완전하게 알 수 없다
📌 인간은 π를 통해 무한에 다가가지만, 도달하진 못한다.
🌀 2. 무한은 아름다운 공포
- 무한(∞)은 수학에서 가장 매혹적인 개념이면서도,
가장 두렵고 난해한 존재 - 파이는 무한을 수치화한 대표적 사례
그래서 파이를 바라보는 건,
무한을 들여다보는 창을 여는 일이다.
🎯 3. 파이는 완전함을 상징하면서도, 도달할 수 없는 존재
- 원은 가장 대칭적이고, 아름다운 도형
- 파이는 그 원을 수치화한 값
→ 그래서 파이는 완전함의 상징
하지만 동시에, 파이의 실체는 계산 불가능한 무한
→ 그래서 파이는 영원히 미완의 수
“우리는 완전함을 갈망하지만, 실제로는 닿지 못한다.”
이 아이러니가 바로 인간 존재의 역설이기도 하다.
🧠 4. 파이는 인간 인식의 경계를 드러낸다
- 수학은 가장 논리적이고 냉철한 언어
- 그 수학 속에서조차 완전히 표현되지 않는 수, π
📌 이건 인간의 이성과 수학조차 닿지 못하는 영역이 존재함을 보여준다
파이는 “모든 것을 아는 건 불가능하다”는
지적인 겸손을 가르쳐 준다.
📚 5. 파이는 인간의 끝없는 사유를 자극한다
- 파이를 외우려는 시도
- 파이의 본질을 증명하려는 수학자
- 파이를 문학과 예술로 재해석하는 철학자
그 모든 시도는
"이해할 수 없음을 이해하려는" 인간의 존재 방식이다.
✍️ 마무리하며
π는 무한함과 완전함,
이해와 불가능성,
그 모순을 안고 있는 수다.
그래서 π는 수학자뿐 아니라, 철학자와 예술가 모두에게 영감을 주는 존재다.
파이를 이해하려는 모든 시도는, 결국 인간 자신을 이해하려는 여정이기도 하다.
🎉 π 시리즈 완결!
이 여섯 편의 시리즈를 통해
단순한 원주율이 아니라,
역사, 수학, 자연, 문화, 철학까지 관통하는 거대한 사유의 여정을 함께 걸었다.

'바로 써먹는 수학픽' 카테고리의 다른 글
| 📘 [생활 속의 수학 ②] 릴 한 바퀴에 감기는 줄의 길이, 수학으로 계산해볼까?– 원주율과 비례식의 실제 (5) | 2025.05.07 |
|---|---|
| 📘 [생활 속의 수학 ①] 낚싯줄을 던졌더니 함수가 따라왔다?– 포물선과 이차함수의 실제 (0) | 2025.05.07 |
| 📘 π 시리즈 ⑤파이와 인간 – 암기, 기념일, 문화 속의 π (0) | 2025.05.05 |
| 📘 π 시리즈 ④파이는 어디에나 있다 – 자연과 과학 속의 파이 (0) | 2025.05.05 |
| 📘 π 시리즈 ③무리수와 초월수 – 파이는 왜 끝이 없는가? (0) | 2025.05.05 |



