'지구의 크기 측정'은 지구의 무엇을 측정한다는 것일까?
대답은 대체로 1)지구의 부피, 2)지구의 지름 또는 반지름, 3)지구의 둘레 정도이다. 그런데 단원명을 다시 보자. --->지구의 크기 측정. 측정이라는 것은 무엇인가? 자, 각도기, 온도계 등의 측정도구를 이용하여 측정한다는 것이다. 지구의 크기를.
그게 가능한가? 그렇다면 다시 질문해보자. 도대체 지구의 무슨 크기를 측정한다는 것인가?
먼저 크기란 무엇인가?
크기라는 말은 '얼마나 큰지'를 나타내는 아주 일반적인 표현이다.
하지만 어떤 대상을 보고 있느냐에 따라 구체적인 의미가 달라진다.
예를 들어보자:
| 책상 | 길이, 폭, 높이 (세로·가로·높이) |
| 풍선 | 반지름, 부피 (얼마나 부풀었는지) |
| 사람 | 키(신장), 몸무게 등 |
| 원 | 반지름, 지름, 둘레, 넓이 |
| 지구 | 반지름, 둘레, 겉넓이, 부피 |
🌍 지구의 경우 '크기'는?
지구의 크기라고 하면 교과서에서는 주로 다음을 의미한다:
1️⃣ 반지름 (Radius)
→ 지구 중심에서 지표면까지의 거리
→ 가장 기본적인 '크기'의 기준 → 이것만 알면 다른 것도 계산 가능
2️⃣ 둘레 (Circumference)
→ 지구를 한 바퀴 도는 길이 → 에라토스테네스가 구한 것
3️⃣ 겉넓이 (Surface Area)
→ 지구 표면 전체 면적
4️⃣ 부피 (Volume)
→ 지구 전체 속 공간이 얼마나 되는지
---> 그런데 '지구의 크기를 측정'한다고 했으니 측정이 무엇인지 알아보자.
📏 '측정'이란?
- 측정이라는 말은 일반적으로 직접 길이, 무게, 시간 등을 재는 것이다.
→ 자, 줄자, 저울, 시계 같은 측정 도구를 이용하는 것이 원칙이다.
🌍 지구의 크기 측정에서는?
- 우리가 지구 반지름이나 둘레, 부피라고 말할 때
→ 둘레, 부피는 수학적 계산으로 구하는 값이다.
→ 직접 재는 것이 아님 → '계산'이지 '측정'은 아님. - 하지만 반지름은?
→ 사실 직접 반지름을 잴 수는 없음. 왜냐하면 땅속 깊이 중심까지 들어갈 수 없으니까. - 그러면 에라토스테네스는 뭘 했느냐?
→ 지표면(껍질 위)에서 그림자와 각도, 두 도시 간 거리(지표면 위의 호)를 직접 측정.
→ 그리고 이를 이용해 지구의 중심각을 구하고
→ 거기서 둘레 → 반지름을 수학적으로 계산.
에라토스테네스는 1)시에네와 알렉산드리아의 거리를 직접 측정하고 2)막대와 막대의 그림자와의 각을 측정함
이를 토대로 수학적 계산을 하여 지구 반지름을 구해냄.
왜 '반지름'이 중요할까?
- 반지름 하나만 알면 → 둘레, 겉넓이, 부피 다 계산할 수 있음.
→ 그래서 지구의 크기 = 보통 반지름을 구하는 문제로 연결.
잠깐! 고대 그리스인은 어떻게 지구가 둥글다는 것을 알았을까?
기원전 3세기, 고대 그리스의 학자 에라토스테네스는 이미 지구가 둥글다는 사실을 알고 있었다. 고대인들은 아래와 같은 관찰을 통해 지구가 구형임을 추론했다.
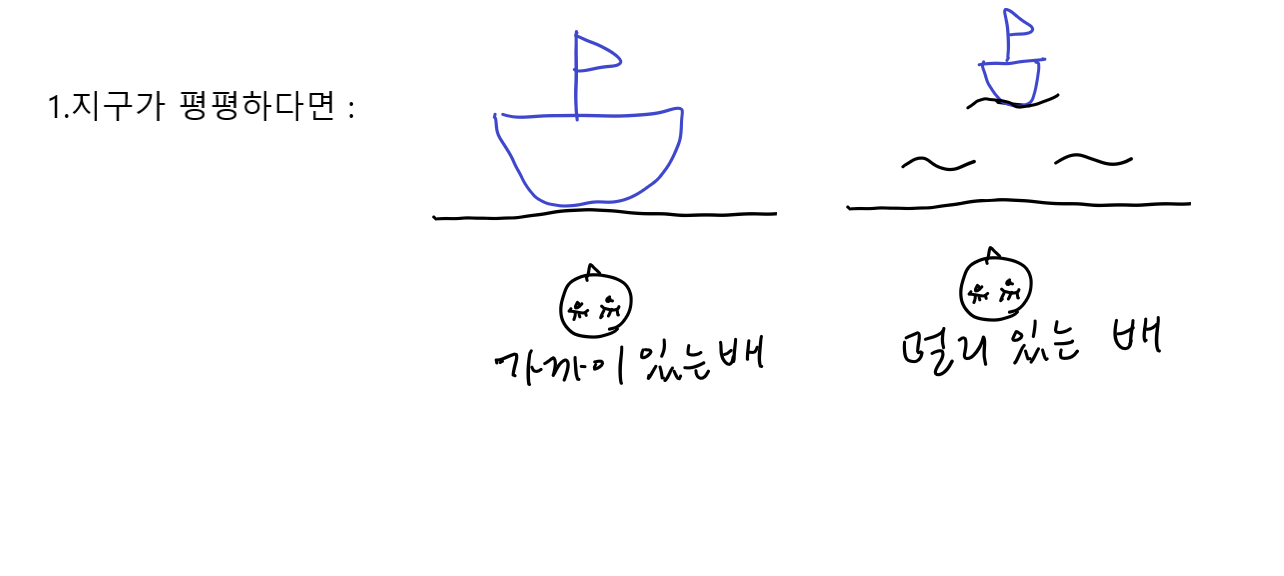
1.항해 시 배가 멀어지면 마스트(돛대)부터 사라지는 모습을 관찰 → 평평하다면 배 전체가 동시에 작아져야 함.

2.월식 때 지구 그림자가 달에 드리워질 때 둥근 그림자가 생김 → 구형의 물체만이 항상 둥근 그림자를 만듦.

3.지구 표면에서 북쪽·남쪽으로 이동하면 별자리의 모양과 보이는 각도가 달라짐 → 평평한 지구에서는 관찰되지 않는 현상.

지구의 크기란 무엇을 말하는 걸까?
교과서에서 말하는 지구의 크기는 여러 가지로 생각할 수 있다:
- 지구의 부피
- 지구의 겉넓이
- 지구의 둘레
- 지구의 반지름
→ 그렇다! 지구의 반지름을 알면 나머지 값들도 계산 가능하다.
→ 지구의 부피:

, 지구의 겉넓이:
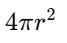
여기서 잠깐! 에라토스테네스는 누구일까?
에라토스테네스 (기원전 약 276~194년)
- 고대 그리스의 학자, 알렉산드리아 도서관 관장
- 지리학, 수학, 천문학, 철학 등 다양한 분야에서 활약
- 소수의 체(에라토스테네스의 체) 개발 → 소수를 효율적으로 구하는 방법
- 최초로 지구의 둘레를 비교적 정확히 계산
📚 어떤 일을 했을까?
1️⃣ 알렉산드리아 도서관 관장
- 고대 세계에서 가장 크고 유명했던 알렉산드리아 도서관의 책임자(관장)였음.
- 엄청난 양의 책과 정보를 정리하고 연구하는 지식의 총사령탑 역할을 함.
2️⃣ 지리학
- 세계 최초로 지구 둘레를 계산한 인물.
- 햇빛과 그림자의 각도, 두 도시 간 거리를 이용해 지구가 둥글고 반지름과 둘레가 얼마인지 추정.
- 그의 계산 결과는 오늘날 값과 약 15% 정도 오차밖에 나지 않을 만큼 매우 정확했음.
3️⃣ 수학
- 에라토스테네스의 체라는 방법을 고안함.
→ 소수(1과 자기 자신만으로 나누어지는 수)를 쉽게 골라내는 방법.
→ 지금도 수학 수업이나 알고리즘 수업에서 자주 사용됨.
4️⃣ 천문학
- 지구의 기울기(자전축의 경사각)도 계산함 → 태양과 별의 움직임 관찰을 통해 구함.
5️⃣ 기타 업적
- 세계 지도 제작에도 기여함 → 위도와 경도의 개념을 이용해 더 정밀한 지도 제작 가능.
- 여러 분야에서 "전문가의 전문가"로 불릴 정도로 다방면에서 활약.

🏆 왜 중요한 인물일까?
- 단순한 관찰과 논리적 사고만으로 지구 크기를 계산한 최초의 인물.
→ 과학적 사고의 대표적인 예시.
→ 실험 기구 없이도 "관찰과 수학"으로 우주의 비밀을 풀 수 있다는 걸 보여줌. - 소수의 체는 오늘날 컴퓨터 프로그래밍, 암호학 등에서도 활용됨.
- 지리학의 아버지로 불릴 정도로 지구와 세계에 대한 인간의 인식 수준을 한 단계 올려놓은 인물.
어떻게 지구의 반지름을 구했을까?
에라토스테네스는 다음과 같은 두 가지를 가정하고 계산:
- 지구는 완전한 구형이다.
- 햇빛은 평행하게 지구에 도달한다.
→ 그리고 한 가지 더, 우리가 지구 단면을 원(대원)으로 보고 계산한다는 전제가 암묵적으로 들어가 있음.
자 그렇다면, 에라토스테네스는 무엇을 측정했을까?
1) 시에네(현재의 아스완)와 알렉산드리아의 거리 : 약 925km
2) 알렉산드리아에서 세운 막대와 막대 그림자 사이의 각 : 약 7.2도

에라토스테네스는 측정한 두 개의 값(시에네와 알렉산드리아 사이의 거리, 막대와 그림자 사이의 각도)을 이용하여 지구 반지름을 계산한다. 그런데 여기서 계산 전에 알아둬야 할 수학 상식 두 가지를 알고 가자.
1) 엇각
에라토스테네스가 아무리 똑똑해도 지구의 중심까지 들어가서 중심각을 잴 수는 없는 노릇, 그래서 지구 밖에서 엇각을 이용하여 지구 중심각을 알아냄. 즉 각A 대신 각A'를 측정함.
- 엇각: 서로 평행한 두 직선에 교차선이 그어질 때 생기는 마주보는 각 → 크기가 같음.

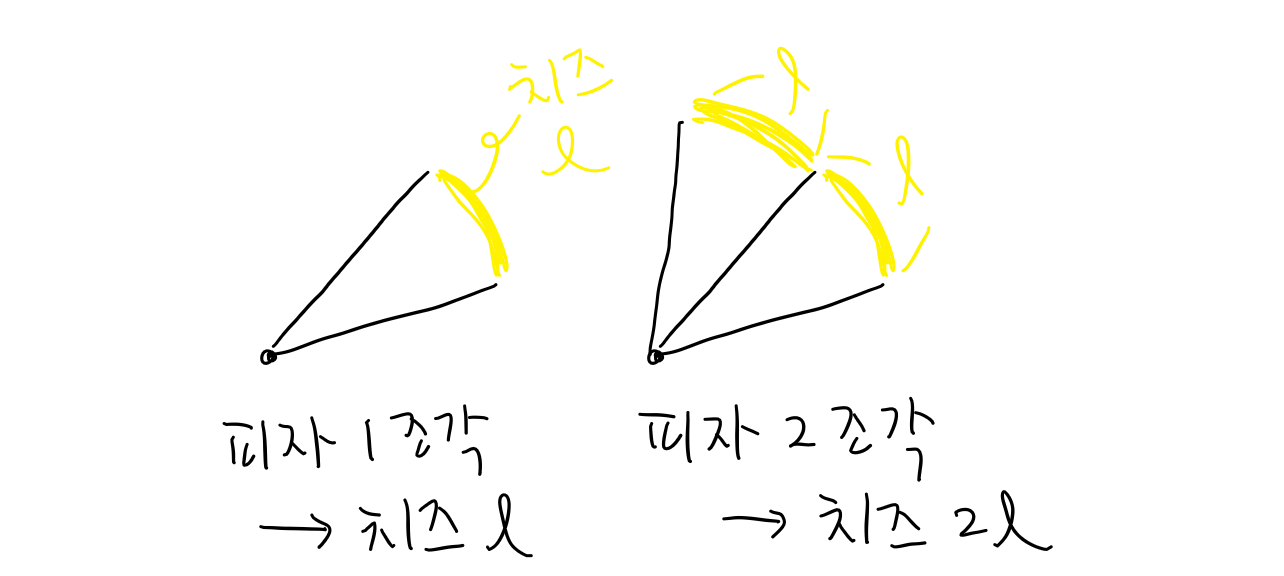
중심각과 호의 비례란?
- 원에서 중심각이 크면 호의 길이도 길어짐.
- 중심각과 호의 길이는 비례:
자 이제 측정한 값과 수학 도구(엇각, 중심각에 호의 길이 비례, 비례식)를 이용하여 지구의 반지름을 계산해보자.

실제 계산 결과
- 에라토스테네스가 구한 지구 둘레: 약 46,000 km
- 오늘날 지구 둘레: 약 40,075 km
→ 약 15% 오차 → 당시 측량 기술과 거리 측정 방법을 고려하면 매우 정확한 결과.
오차가 발생한 이유는?
- 도시 간 거리 측정의 오차 → 도보, 낙타 이동으로 추정한 거리
- 지구가 완전한 구형이 아님 → 약간 납작한 타원체(적도 부근이 약간 더 넓음)
- 태양의 고도 측정에서 약간의 오차 발생 가능성 → 고대 측정 기구의 한계
이렇게 에라토스테네스는 수학적 사고력과 관찰력으로 약 2200년 전 이미 지구의 크기를 매우 정확하게 계산했다. 이는 과학적 사고의 힘과 수학의 응용 가능성을 보여주는 대표적 사례로 이 단원에서는 단지 지구의 반지름을 구하는 데 그치지 말고 에라토스테네스의 자취를 따라가며 그가 어떻게 이런 생각을 해냈는지 우리도 한 번 질문하고 깊이 고민하는 시간이 되었으면 좋겠다.
'질문이 있는 과학픽' 카테고리의 다른 글
| 📘(1편) 라부아지에는 어떻게 물 분해 실험을 할 생각을 했을까? -산소 혁명을 이룬 과학자 [연금술의 시대를 끝낸 사람, 라부아지에] (0) | 2025.06.16 |
|---|---|
| 🔥(2편)라부아지에는 어떻게 물 분해 실험을 할 생각을 했을까? -산소 혁명을 이룬 과학자 - [산소를 산소라 부른 사람, 라부아지에] (0) | 2025.06.16 |
| 위성이 알려주는 지구의 중심 - 지구중심 4편 (0) | 2025.05.19 |
| 지구 중심은 어떻게 알았을까? -지구중심 3편 (0) | 2025.05.19 |
| 지구 중심은 어떻게 계산했을까? -지구중심2편 (0) | 2025.05.18 |



