반응형
고대 바빌로니아부터 슈퍼컴퓨터 시대까지, 파이를 계산하려는 인간의 노력은 멈춘 적이 없습니다. 파이 계산의 역사와 인간의 지적 도전정신을 따라가 보세요.
🔍 왜 인간은 파이를 계산해 왔을까?
아무리 큰 원이든 작은 원이든,
‘둘레 ÷ 지름’은 항상 같다.
이 간단한 진리를 깨달은 순간부터, 인류는 ‘얼마나 정확하게 그 값을 알 수 있는가’에 집착해왔다.
파이는 단지 숫자가 아니라, 완벽을 추구하는 인간의 욕망의 역사다.
🏺 1. 고대 바빌로니아와 이집트 – 대충 '3'이면 되지
- 기원전 1900년경, 바빌로니아인들은
π ≈ 3.125 로 계산했어. - 이집트의 Rhind 파피루스에는
π ≈ 3.1605 로 추정한 기록이 있어.
👉 지금 우리가 보는 파이보다 단순했지만, 건축과 토목에선 충분히 쓸 수 있었던 수준
🏛️ 2. 그리스 – 아르키메데스의 혁신
- 아르키메데스는 원 안과 원 밖에 정다각형을 넣고
그 둘레를 계산함으로써 파이를 추정했어. - 그는 96각형까지 사용해
3.1408 < π < 3.1429
라는 경이로운 추정치를 제시!
📌 이건 기하학 기반의 엄청난 계산 능력을 보여주는 사례야.
👉 “정확한 파이”를 향한 첫 과학적 접근이라 할 수 있지.
🧭 3. 중국 – 조충지의 천재적 계산
- 남북조 시대(기원후 5세기)의 수학자 조충지(祖沖之)는
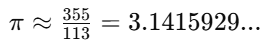
라는 놀라운 수치를 제시했어.
👉 이 수치는 1000년 이상 세계에서 가장 정확한 파이값으로 인정받았고,
조충지는 “파이의 제왕”이라 불려.
🕯️ 4. 중세와 이슬람 수학자들 – 잊히지 않은 열정
- 중세 유럽에선 수학의 발전이 느렸지만,
이슬람권에서는 파이에 대한 연구가 계속되었어. - 알 카시(Al-Kashi)는
16자리 소수까지 π를 계산해냈고,
"하늘은 수학으로 가득하다"고 말했지.
📐 5. 유럽 르네상스 – 파이의 기호가 태어나다
- 1706년, 영국 수학자 윌리엄 존스(William Jones)가
처음으로 π를 지금처럼 π라는 기호로 사용했어. - 이후 오일러(Euler)가 이 표기법을 널리 퍼뜨리며 정착시켰지.
👉 그 전까지는 π 대신 "원주비" 같은 표현을 썼다는 사실, 흥미롭지?
💻 6. 현대 – 컴퓨터와 무한을 향한 전쟁
- 1949년, 전자식 컴퓨터 ENIAC은 π를 2037자리까지 계산
- 이후 슈퍼컴퓨터와 알고리즘이 발전하면서
2023년 기준, 100조 자릿수 이상이 계산됨! - 사용된 알고리즘:
- Machin-like formula
- Gauss–Legendre algorithm
- Chudnovsky algorithm
📌 지금도 π 계산은 세계의 수학자·컴퓨터 과학자들이 경쟁하는 분야야.
숫자 자체보다, 어떤 방식으로 더 효율적으로 계산할 수 있는지가 핵심!
✍️ 마무리하며
“π는 하나의 숫자지만, 그 숫자를 향한 인류의 여정은 하나의 문명이다.”
파이를 계산한다는 건
단순히 계산하는 게 아니라, 우주가 어떻게 작동하는지를 이해하려는 시도야.
그리고 그 여정은 지금도 계속되고 있어.

📗 다음 편 예고
시리즈 ③: “무리수와 초월수 – 파이는 왜 끝이 없는가?”
: 이제 파이를 단순한 역사적 수치가 아니라,
수학적으로 ‘표현 불가능한 수’로 탐구해볼 거야.
'바로 써먹는 수학픽' 카테고리의 다른 글
| 📘 π 시리즈 ③무리수와 초월수 – 파이는 왜 끝이 없는가? (0) | 2025.05.05 |
|---|---|
| 🎯 왜 파이(3.14...)가 180도일까? (1탄)수학을 좋아하든 말든, 이건 누구나 궁금한 이야기 (0) | 2025.05.05 |
| 📘 π 시리즈 ① | 파이란 무엇인가?– 단순한 숫자 그 이상, 수학이 품은 무한한 원 (0) | 2025.05.05 |
| 학생들이 좋아한 수학이론 ⑤ – 쌍둥이 소수, 무한 속의 짝꿍 -『우리 수학자 모두는 약간 미친 겁니다』 (0) | 2025.05.05 |
| 학생들이 좋아한 수학이론 ④ – 제르맹 소수, 불완전한 수 속의 완벽한 패턴 - 『우리 수학자 모두는 약간 미친 겁니다』 (0) | 2025.05.04 |



